Abdullah Şamil Güser
z-score
\[Z = \frac{X - \mu}{\sigma}\]z-score answers the following question : Is there a difference between the sample proportion (hypothesized) and population proportion (theoretical)?
How much standard deviation I am away from the mean?
Derivation
Linearity of expectation
\[E[aX+b] = aE[X] + b\]Variance property
\[Var[aX+b] = a^2Var[X]\]Applying these formulas, if $X$ is a normal random variable with mean $\mu$ and variance $\sigma^2$, and $Z = (X - \mu)/\sigma$, then;
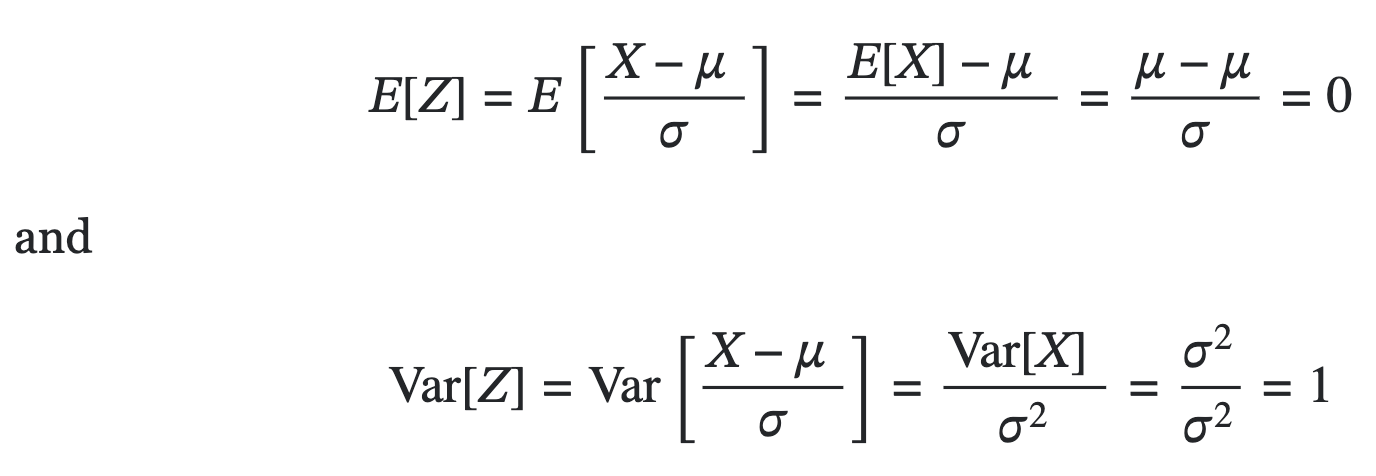
Therefore, $Z$ has mean 0 and variance 1. Also we know that linear transformation of a normal random variable is still normal, therefore $Z$ is standard normal distribution.
One proportion z-test
